METODOS CONGRUENCIALES

Un Generador de números aleatorios es un componente o funcionalidad que crea números o símbolos para un programa sofware en una forma que carezca de un patrón evidente, y que así parezcan ser números aleatorios.

La mayor parte de los generadores de números aleatorios son, en realidad, pseudoaleatorios: se calcula (o introduce internamente) un valor X0, que llamaremos semilla, y, a partir de él, se van generando X1, X2, X3, ...

Siempre que se parta de la misma semilla, se obtendrá la misma secuencia de valores.

El algoritmo básico es el método congruencial123, que genera valores en el intervalo [0,1), mediante el siguiente esquema: Se fijan A, B, enteros positivos (deben tener ciertas propiedades para obtener un buen generador), y, a partir de una semilla X0 en el conjunto 0,1,...,(N-1), se generan X1 = A*X0+B (mod N) X2 = A*X1+B (mod N) X3 = A*X2+B (mod N) ... X(k+1) = A*Xk+B (mod N) ...

donde A*X+B (mod N) es el resto de la división entera de A*X+B entre N. Por ejemplo, 16 (mod 7) es 2.

A partir del método congruencial, es posible tomar valores pseudoaleatorios en el intervalo [0,1) como sigue: Se toma N, entero, muy grande, se toman A, B adecuados, y una semilla X0 en 0,1,..,(N-1). A partir de ella, se generan X1,X2,X3,... por el método congruencial, y a partir de ellos, Y0,Y1,Y2,Y3,... mediante la fórmula Yk = Xk /N

HISTORIA DE LOS NUMEROS ALEATORIOS

Un número aleatorio es un resultado de una variable al azar especificada por una funcion de distribucion. Cuando no se especifica ninguna distribución, se presupone que se utiliza la distribución uniforme continua en el intervalo [0,1).

En los ordenadores personales es fácil simular la generación de números aleatorios, mediante mecanismos de generación de nùmeros seudoaleatorios, que, sin ser aleatorios (siguen una fórmula), lo aparentan. 

para conocer sobre la historia de los numeros aleatorios haga clic en el siguiente enlace:

http://redalyc.uaemex.mx/src/inicio/ArtPdfRed.jsp?iCve=85200804

DISTRIBUCIONES CONTINUAS Y DISCRETAS

 

 DISTRIBUCIONES CONTINUAS

Es una variable que puede tomar tanto valores enteros como fraccionarios.

Es generada por una variable continua (x).

f(x)³ 0 Las probabilidades asociadas a cada uno de los valores que toma x deben ser mayores o iguales a cero. Dicho de otra forma, la función de densidad de probabilidad deberá tomar solo valores mayores o iguales a cero. La función de densidad de probabilidad sólo puede estar definida en los cuadrantes I y II.

                                                                                        

La sumatoria de las probabilidades asociadas a cada uno de los valores que toma x debe ser igual a 1. El área definida bajo la función de densidad de probabilidad deberá ser de 1.

Hasta el momento se han considerado las distribuciones de probabilidad para variables discretas, donde se podía asignar el valor que toma la función de probabilidad cuando la variable aleatoria tomaba un valor en concreto. Sin embargo, al considerar las variables continuas se encuentra uno el problema de que, lo más probable, los datos que se puedan recabar no sean completamente exactos, o dos o más de ellos no coincidan, por lo que se tienen que trabajar en intervalos y, en ese momento, modelar una función se convierte en un problema serio.

Las distribuciones continuas son aquellas que presentan un número infinito de posibles soluciones:

Ejemplo: El peso medio de los alumnos de una clase puede tomar infinitos valores dentro de cierto intervalo (42,37 kg, 42,3764 kg, 42, 376541kg, etc); la esperanza media de vida de una población (72,5 años, 7,513 años, 72, 51234 años).

DISTRIBUCIONES DISCRETAS

Las distribuciones discretas son aquellas en las que la variable puede pude tomar un número determinado de valores:

Ejemplo: si se lanza una moneda al aire puede salir cara o cruz; si se tira un dado puede salir un número de 1 al 6; en una ruleta el número puede tomar un valor del 1 al 32.

 MAPA DE DISTRIBUCIONES

En el siguiente enlace encontraras algunas de las distribuciones continuas y discretas: 

https://docs.google.com/document/d/1D8CDX7y1iZfrzC_NNvKDcEEeElOG1CvbKlMkcsxp6wU/edit?hl=en&pli=1#

Simulación

La simulacion es una imitacion de la realidad sin que implique vivirla. La magia que implica la simulacion es que se parece mucho a la realidad sin ser la realidad.

Un ejemplo de esto lo vivimos en la naturaleza como los camaleones, que simulan ser algo que no son.

Ventajas y Desventajas de la Simulación

VENTAJAS

• Es un proceso relativamente eficiente y flexible.
• Puede ser usada para analizar y sintetizar una compleja y extensa situación real, pero no puede ser empleada para solucionar un modelo de analisis cuantitativo convencional.
• Los directivos requieren conocer como se avanza y que opciones son atractivas.
• La simulacion no interfiere en sistemas del  undo real.
• Permite estudiar los efectos interactivos de los componentes individuales o variables para determinar las mas importantes.

DESVENTAJAS

• Un buen modelo de simulación resulta bastante costoso.
• La simulacion no genera soluciones optimas a problemas de analisis cuantitativos, en técnicas como cantidad economica de pedido, programacion lineal o PERT. Por ensayo y error se producen diferentes resultados en reprtidas corridas en el computador.
• Los directivos generan todas las condiciones y restricciones para analizar las soluciones al modelo de simulación no produce respuestas por si mismo.
• Cada modelo de simulación es unico.

Ventajas y Desventajas de la Experimentación

Ventajas 

1 La asignación aleatoria de las unidades de análisis a los grupos experimental y control permite controlar la validez interna del experimento.

2 Las posibles diferencias que manifiesten en los grupos son producto de la casualidad.

3 La utilización de la preprueba permite cuantificar el cambio inducido por el tratamiento experimental.

4 La asignación por pareamiento aleatorio permite controlar las diferencias entre las unidades de análisis.

Desventajas

1 La validez interna pudiera ser afectada por la preprueba.

2 El pareamiento aleatorio es útil cuando se trabaja un experimento en el que los grupos estan integrados por 12 o 14 unidades de análisis, es decir, es aplicable en grupos pequeños.

Bibliografía: Introducción a la metodología de la investigación; Héctor Luis Ávila Baray

Medidas de Tendencia Central

 MEDIA

En ,matematica y estadistica, la media aritmética (también llamada promedio o simplemente media) de un conjunto finito de números es igual a la suma de todos sus valores dividida entre el número de sumandos. Cuando el conjunto es una muestra aleatoria recibe el nombre de media muestral siendo uno de los principales estadìsticos muestrales.

Expresada de forma más intuitiva, podemos decir que la media (aritmética) es la cantidad total de la variable distribuida a partes iguales entre cada observación.

Por ejemplo, si en una habitación hay tres personas, la media de dinero que tienen en sus bolsillos sería el resultado de tomar todo el dinero de los tres y dividirlo a partes iguales entre cada uno de ellos. Es decir, la media es una forma de resumir la información de una distribución (dinero en el bolsillo) suponiendo que cada observación (persona) tuviera la misma cantidad de la variable.

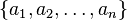Dados los n números , la media aritmética se define simplemente como:

MEDIANA

la mediana es el valor de la variable que deja el mismo número de datos antes y después que él, una vez ordenados estos. De acuerdo con esta definición el conjunto de datos menores o iguales que la mediana representarán el 50% de los datos, y los que sean mayores que la mediana representarán el otro 50% del total de datos de la muestra. La mediana coincide con el percentil 50, con el segundo cuartil y con el quinto decil.

MODA

Esta medida de posición se asocia con el valor más común, más típico o que ocurre más frecuentemente en un conjunto de datos. Más concretamente, se define como el valor al cual corresponde la mayor frecuencia. En la serie que se incluye seguidamente se puede observar que la moda es 21.

14,14,17,17,21,21,21,21,33,36,40

La moda es una medida muy natural para describir un conjunto de datos; su concepto se adquiere fácilmente: es el sueldo más común, el peso más corriente, la edad más frecuente.  Además, tiene la ventaja de que no se ve afectada por la presencia de valores altos o bajos.

La principal limitación esta en el hecho de que requiere un número suficiente de observaciones para que se manifieste o defina claramente. La moda se puede aplicar tanto a datos cualitativos como cuantitativos.