Medidas de Tendencia Central

 MEDIA

En ,matematica y estadistica, la media aritmética (también llamada promedio o simplemente media) de un conjunto finito de números es igual a la suma de todos sus valores dividida entre el número de sumandos. Cuando el conjunto es una muestra aleatoria recibe el nombre de media muestral siendo uno de los principales estadìsticos muestrales.

Expresada de forma más intuitiva, podemos decir que la media (aritmética) es la cantidad total de la variable distribuida a partes iguales entre cada observación.

Por ejemplo, si en una habitación hay tres personas, la media de dinero que tienen en sus bolsillos sería el resultado de tomar todo el dinero de los tres y dividirlo a partes iguales entre cada uno de ellos. Es decir, la media es una forma de resumir la información de una distribución (dinero en el bolsillo) suponiendo que cada observación (persona) tuviera la misma cantidad de la variable.

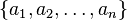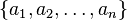Dados los n números , la media aritmética se define simplemente como:

MEDIANA

la mediana es el valor de la variable que deja el mismo número de datos antes y después que él, una vez ordenados estos. De acuerdo con esta definición el conjunto de datos menores o iguales que la mediana representarán el 50% de los datos, y los que sean mayores que la mediana representarán el otro 50% del total de datos de la muestra. La mediana coincide con el percentil 50, con el segundo cuartil y con el quinto decil.

MODA

Esta medida de posición se asocia con el valor más común, más típico o que ocurre más frecuentemente en un conjunto de datos. Más concretamente, se define como el valor al cual corresponde la mayor frecuencia. En la serie que se incluye seguidamente se puede observar que la moda es 21.

14,14,17,17,21,21,21,21,33,36,40

La moda es una medida muy natural para describir un conjunto de datos; su concepto se adquiere fácilmente: es el sueldo más común, el peso más corriente, la edad más frecuente.  Además, tiene la ventaja de que no se ve afectada por la presencia de valores altos o bajos.

La principal limitación esta en el hecho de que requiere un número suficiente de observaciones para que se manifieste o defina claramente. La moda se puede aplicar tanto a datos cualitativos como cuantitativos.